Solid Hydrogen Fueling of an Air Breathing Supersonic Combustor
40 Nutmeg Lane
Glastonbury, CT 06033
Abstract
Wall injection of solid H2 particles into the supersonic airstream of a combustor has been investigated to determine if it can provide ultrafast distributed fuel mixing for a practical large scramjet engine [1]. It is practical to pump and inject the solid as a 4 K solid H2/liquid He slurry with a very low He fraction. High-speed single H2 pellet injection into an inert gas has been performed to examine solid H2 particle ablation phenomena and to compare with modeling predictions. Modeling of a solid H2 particle ablating in a Mach 3 flow has been done to define ablation physics, to predict particle lifetime, and to define the dependence of particle lifetime on the parameters of the problem. Slurry jets are expected to provide adequate penetration of the supersonic free stream. H2 ablation and mixing is shown to be extremely rapid, although quantitative supersonic ablation rates could not be derived from high-speed pellet injection experiments.
Introduction
Efficient propulsion at high mach numbers must use air-breathing engines to avoid the mass penalty of carrying oxidizers. Subsonic combustors operating at M>1 are impractical because of the shock losses. Fundamental problems of supersonic combustion include: 1) fuel distribution and mixing, 2) drag losses from protruding structures, and 3) the low fraction of combustion energy relative to exhaust kinetic energy and consequent low tolerance for losses. The most difficult problem of supersonic combustion is to perform both volumetric mixing and full reaction during the very short residence times of the combustor.
This work investigates the feasibility of wall injected solid H2 scramjet fueling. Solid H2 fueling has crucial advantages: 1) wall injected solid particles can penetrate the flow over the width of the combustor, and 2) gas and liquid shedding from the moving solid results in extremely fast volumetric mixing.
Specific Objectives
The goal of this program was to lay the foundation for demonstrating the feasibility of solid H2 particle scramjet fueling. Modeling of the flow, mass and energy of a single H2 pellet moving at supersonic speed relative to a gas was done to predict ablation parameters. Experiments imaging a H2 pellet injected into vacuum, helium (He), and nitrogen (N2) at a speed of 1 km/s were performed to demonstrate real solid H2 ablation rates. Examination of particle cross-jets in a supersonic flow was done to determine the necessary jet parameters for supersonic distribution and mixing. Engineering analysis was done to assess the overall practicality of the technique.
Results and Discussion.
The primary advantages of solid H2 fueling are: 1) the fuel can be injected much farther into a flow than is possible with a liquid spray, covering a much larger volume in a shorter time, 2) wake mixing behind a small particle and liquid ablation would result in rapid dispersion of H2 across the pellet trajectory in the combustor, improving mixing well beyond present concepts that depend on wake mixing of the entire injection jet, 3) wall injection would eliminate protruding injector drag, 4) it may be possible to inject the solid at high velocity and use its kinetic energy to augment thrust, and 5) the fuel density is higher and beneficial additives can be injected with the fuel.
Particle Jets. Previous supersonic jet injection studies have elucidated a number of the processes of liquid jet breakup. Breakup of the jet is initiated when the liquid jet emerging from the injector becomes unstable; axial waves form on the jet column, these are amplified, and the waves cause the column to fracture. A liquid jet must have an injection momentum greater than a certain minimum to penetrate the supersonic stream. The q of the injected stream must be greater than 6, where q is defined as: q = (ρ jvj2/ρ eve2) where the subscript j refers to the jet, and the subscript e refers to free stream values [2]. There are 3 basic zones in jet breakup: the cohesive jet zone, the spray formation zone, and the atomization zone.
The physics of a large-particle jet are very different from a liquid jet. For solid H2 particle injection the particle size would be on the order of 1 mm, and the particle loading would be very high (> 80%), in the form of a solid H2/liquid helium slurry. The q requirements for jet penetration and stability will be lessened significantly; the particle diameter is larger than the wavelength of the jet surface instabilities (about 1/3 mm). Large (> 10 micron) particle jet injection into supersonic flows has never been studied for the reason that there was no way to burn up such large particles rapidly. A liquid jet with a 30% loading of 3-5 micron sand particles has been investigated, finding significant penetration of the particles beyond the liquid in the jet [3]. There have also been indications that the particles stabilize the jet column. A H2 slurry jet also has a low specific gravity (solid H2 0.09 g/cm3; sp. gr. 0.1). Previous experiments used particles with a specific gravity of 3 or higher.
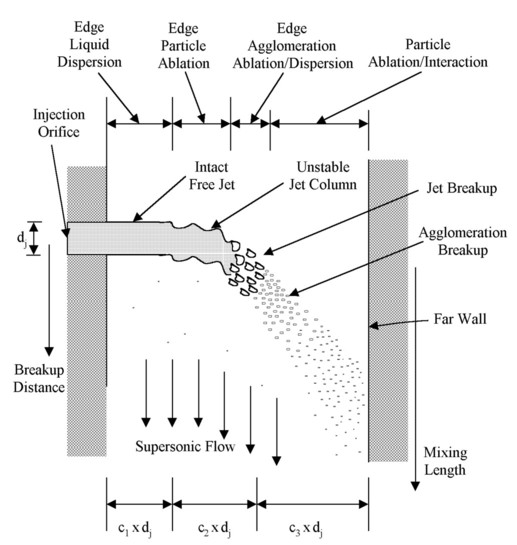
Figure 1. Schematic of injection of a particle jet into a supersonic flow.
A schematic of the injection process and breakup of a particle jet is shown in Fig. 1. The jet is made up primarily of particles with a minor liquid volume fraction. After entering the supersonic stream the particle jet column quickly (but much more slowly than a liquid jet) develops wave instabilities on its surface that lead to breakup of the jet [4]. The jet will break into agglomerations of particles of varying size, which continually decrease in size, ending in a cloud of individual particles that then ablate. The liquid and gas ablated from the particles is mixed and combusted as an end to the ablation process. The phenomena associated with combustion at the jet and its effects have not yet been addressed. This figure shows how the fuel jet would penetrate the entire duct. For jet development as shown most of the mixing would take place at the far end of the jet.
Based on the density of solid H2, a flow velocity of 170 m/s would be required for a solid H2 jet to reach a q value of 6 to fully penetrate a Mach 3 flow at 10,000 m altitude. For a 1 mm diameter H2 particle in a 1 km/sec, 1 atm air flow, ReD = 1 x 105 and CD = 0.4. This leads to a force of 0.5 N on the particle for a 0.6 MPa dynamic pressure, and implies an acceleration of 4 x 106 m/s2. For this magnitude of acceleration the particle will reach 1000 m/s velocity in about 1 ms. The 10 m long combustor transit time of the flow is about 10 ms. The time to accelerate the 1 mm particle to flow speed is small compared with this, so that 10 ms would be the residence time of any H2 particle smaller than about 1 mm. A 10 ms residence time for a 100 m/s injection cross-velocity implies that the particles penetrate the full 1 m width of the combustor.
Solid H2 Slurries. A very large mass flow rate is required for scramjet propulsion to achieve large thrusts. Experimental studies of high-speed centrifugal pumping of a H2 slush (coexisting solid and liquid H2) that were done at the NBS by Daney et.al. [5] showed that the slush pumping characteristics were the same as for the liquid for all pump characteristics and for both aged and fresh slushes for a solid fraction from 0.19 to 0.55. Slush H2 (a mixture of solid H2 and liquid H2) has already been extensively investigated [e.g. 6]. A solid H2, liquid He (sH2/lHe) slush can be made at the 4 K boiling point of liquid He, stabilizing both the solid H2 particles against thermal recrystallization and stabilizing energetic materials mixed into them. A small fraction of He added to a propellant does not a significantly reduce rocket thrust [7]. Recent work on sH2/lHe slurries has been done at NASA Glenn.
The Physics of H2 Ablation. Previous research [8] revealed the existence of physical mechanisms that should result in such rapid ablation of solid H2 particles that these particles could be used to fuel a scramjet combustor. Simple analyses of the lifetime of 1 mm diameter particles result in limits that are so broad that more detailed modeling has been required to provide even an approximate lifetime prediction. The problem of solid H2 particle ablation in a combustion gas environment is extremely complex even compared with standard ablating particle modeling [9].
The primary controlling physical phenomena of H2 ablation are: 1) H2 gas is evolved as a result of heat flux to the liquid surface, decreasing and controlling this heat flux, 2) N2 and H2 counter diffuse; there is a zero concentration of N2 at the pellet surface; N2 condenses in the layer, 3) There is a flow of pure H2 gas near the pellet parallel to the free stream flow around the pellet, 4) There is a flow of H2/N2 gas mixture between the H2 flow and the free stream flow, and 5) There is a flow of very low viscosity H2 liquid on the pellet surface parallel to the H2 gas flow.
Certain characteristics of the solid H2 ablation problem are unique, however. The existence of absolute low temperatures leads to the most important difference between solid H2 and normal ablation. In common ablation, temperatures vary from 300 K in the free stream to 2000 K at the ablating surface. Behind a M=3 shock in STP air the temperature is on the order of 800 K, so that there is a temperature ratio of 2.5 between the flow next to the body and a body at STP. In the case of solid H2 the temperature varies from 800 K (without combustion) to 30 K, the boiling point of H2 at 4 atm pressure. This represents a temperature ratio of 27. The importance of this difference in temperature ratio across the layer is that all of the diffusion coefficients vary as T2. For high temperature ablation T2 is a factor of 6, where the slowest diffusion is at the free stream edge of the layer. In the case of solid H2 T2 is a factor of 730, and another factor of 10 higher in a combustion-heated atmosphere. This means that the entire ablation process in the gas phase is rate limited by diffusion in the cold regions near the surface. Also note that the species diffusion ends (as a gas) at a temperature of 95 K for N2, a factor of 3 higher temperature than the liquid temperature and a factor of 10 higher diffusivity than at the surface.
Another complication is the existence of temperatures near the body at which the free stream gases condense to a liquid. Although the times scales are short, condensation will probably occur near the surface and cause a significant heat release there. Even this phenomenon might be thought to be included in the problem of reacting, ablating surfaces, but the interaction between the species diffusion and temperature profiles means that the energy and species equations are coupled, and the standard assumption of frozen boundary layer heat transfer cannot be used.
The liquid layer adds complexity to the overall flow description in the case of the supersonic H2 particle injection because the liquid H2 layer flows much faster than in the standard ablation problem. The two causes for this rapid flow are 1) the low viscosity of the liquid (order of magnitude less than common liquids), and 2) the strong pressure gradient that penetrates all of the boundary layer flows. The flow of liquid is a significant factor in the overall ablation process.
Real scramjet fueling will involve cross injection into a supersonic stream and particle stream evolution from a continuous, dense, jet of large particles to separated, ablating particles. There has never been modeling or experimental research on a large particle, high solids loading, high-speed jet. Both pellet injection and pellet jet problems involve high speed flow past a particle, but in a pellet injection experiment there is a single shock wave in front of the pellet with flow in basically one direction, whereas in the real injection case there is complex break-up process with multiple shocks interacting with many particles in a supersonic cross flow.
Heat Transfer Calculations. The heat transfer is critically important because it determines not only the overall ablation rate of the H2, but the flows around the pellet also. In assessing what physical mechanisms control the process of pellet vaporization, the magnitudes of the heat sources and sinks must be estimated. For the H2 the significant heat sinks are the heat of fusion, Qf, and the heat of vaporization, Qv. QfH = 0.6 x 105 J/kg and QvH = 4.5 x 105 J/kg. Thus the total heat needed for evaporation from the solid is approximately (neglecting small specific heat contributions) QtH = 5.1 x 105 J/kg. The total heat required to vaporize the entire pellet is thus 1.9 J; only 0.25 J is required to melt it.
For a chamber with a nominal length of 1 m, a injected pellet will displace a column of gas 1 m long and 3.2 mm in diameter, or 8 x 10-6 m3 of gas. The mass of gas in the displaced column of gas is 8 x 10-6 kg, and the gas temperature is 800 K. The heat in the column based on heat capacity is Q = 6.5 J. Thus, if all of this heat were absorbed into the pellet, it would be fully vaporized in a pathlength of about 30 cm, or simply melted in about 4 cm. Most of this energy flows around the pellet; only a small fraction diffuses to the liquid surface to melt the pellet. In terms of the heating rate, the pellet passes through the 1 m column in 1 ms, so that the potential heat deposition is 6.5 kw. For the case of H2 ablation Te is 800 K and Tm is 14 K, so that the temperature continually decreases from its free stream value. The steep temperature gradients are near the pellet surface as a result of the much lower diffusivities. There is an inflection point near the surface also as a result of condensation heat release.
One way to estimate the heat transfer is to assume pure conductive heat transfer over an appropriate thickness of the layer. The conductivity would be determined by the average temperature, and the temperature difference would be determined by that across the diffusion limited section of the layer. Assuming a temperature gradient thickness δ of 10-6 m, a thermal conductivity of H2 at 50 K of 0.04 W/m-K, then a temperature difference of 50 K gives a heat transfer rate of Q = k Δ T/δ = 2 x 106W/m2. The heat transfer to the H2 liquid layer is another controlling parameter for the overall pellet ablation.
Considering the regression rate of the melt-solid interface a linear temperature gradient through the liquid layer from the freezing (14 K) to the boiling temperature (30 K) implies a heat flux of q = 1.7 /tlH2 J/m2-s (tlH in m, klH2 = 0.11 W/m-K). Assuming a liquid layer thickness on the order of 1 micron implies a heat flux of q = 1.7 x 106 W/m2 which is on the same order as the heat flux calculated through the gas layer.
The maximum temperature gradient possible through the gas layer above the liquid layer is a linear gradient between the boiling temperature at one atm (20 K) and the condensation temperature of the combustion gas, taken to be 50 K (significant subcooling is expected to take place. The maximum heat flux is thus for kHg = 0.030 W/m-K, qmax = 0.9/tg1H J/m2-s (tg1H in m). Thus, the gas layer that extends from 20 to 50 K in the gas temperature diffusion profile of H2 must also be on the order of microns thick to melt the pellet.
The maximum temperature gradient possible through the inter-diffusing gas layer above the H2 gas layer is a linear gradient between 50 K and 2000 K. Since the thermal conductivity of H2 gas is a factor of ten more than that for N2. qmax = 200/tg2H J/m2-s, (tg1H in m). Thus, the outer gas layer can be a factor of 200 thicker and still transmit the same amount of heat through the two thin layers near the pellet.
Transient Ablation Analysis. The time scales of the pellet experiment are such that transient effects further complicate the analysis of pellet heat flows. A pellet traveling at a speed of 1 km/s will only require 1 ms to travel 1 m. Thus the first 10 cm of travel into the N2 requires 0.1 ms. At room temperature diffusivities, D, (mass, momentum, and thermal diffusivities are similar) in N2 are of the order of 10-4 m2/s and vary as the square of the temperature. Diffusion times over a length scale d are on the order of d2/D, such that a temperature gradient on the scale of 0.1 mm (1/3 of the shock standoff distance) will require 0.1 ms to diffuse. The full gas boundary layer is 30 microns thick and the cold part 10 microns thick. At the bottom of the H2 gas layer the temperature is a factor of 27 lower and the diffusivity has decreased by a factor of 700, so that the diffusion time for the cold bottom of the boundary layer will be a significant fraction of the residence time period of the pellet. The flow over the pellet has a residence time on the order of 0.01 ms, so that the shock flows are well established very quickly.
Another question is whether there is actually time to condense the free stream gases near the pellet. The residence time of the cold gases near the pellet will be on the order of 0.1 ms, and the collision rate is very high, so condensation will probably occur. Nucleation, subcooling, and the number of collisions required to condense may modify this conclusion.
Pellet Lifetime Estimates. An absolute minimum lifetime of a pellet traveling at M=3 through l atm air can be estimated if it is assumed that all of the air in the pellet's path is condensed to a liquid and the heat released is used to melt the solid H2 which then flows off of the pellet before it vaporizes. Since the heat needed to vaporize H2 is 8.5 times the heat needed to simply melt it, a melting but not vaporizing pellet will require a much lower heat input to ablate.
For a 1 mm diameter pellet moving at vp=1 km/s (M=3) in 1 atm of air, the heat release of the incoming air will be qc= vp(π rp2/2)ρ s (Qva + Cpa Δ Ts) = 1.8 x 103 watts, where ρ s is the density behind a M=3 normal shock, Qva is the heat of condensation of air, Cpa is its specific heat, and Δ Ta the difference between the air temperature behind the shock and its condensation temperature. Ta is assumed to be that behind the normal shock: 800K. The pellet time-average frontal area was estimated to be half of its initial value. Fully 80% of the heat release results from cooling the gas. A minimum particle lifetime is then: tp = (mp)ρ H2)(QvH2)/qc = 1.5 µ s (melting). If the ablation process vaporizes the particle totally, then the minimum particle lifetime is tp = 13 µ s (vaporizing). These are lower bounds on the pellet lifetime.
The heat flux to the pellet is on the order of 106 W/m2, which leads to another estimate of pellet lifetime. This heat flux can be related to the vaporization mass flux assuming that no liquid is lost. The area of the pellet, including its side is 5 x 10-5 m2, so the heating rate of the pellet would be 50 W, and the heat to melt and vaporize is 5.1 x 105 J/kg. The vaporization rate would then be 10-4 kg/s. Since the pellet mass is 4 x 10-6 kg, the pellet lifetime would be about 40 ms. If the pellet were spherical with the same diameter (3.2 mm) its lifetime would be 15 ms. This lifetime would be reduced by a factor of 8 if the pellet was ablated by only liquid shedding.
This lifetime estimate can be checked for consistency in a number of ways. The heating rate derived above if all of the heat in the gas column in front of the pellet was deposited on the pellet is 6.5 kw, which implies that under 1% of this energy actually diffuses to the pellet. This number is consistent with the diffusion calculation that indicated 0.4% of the mass diffused toward the surface.
The flow rate of the mass in the boundary layers around the pellet should also be consistent with this. For a boundary layer thickness of 10 microns at the edge of the pellet, and a velocity of 300 m/s, the volume flow rate is dV/dt = 3 x 10-5 m3/s. The layer is assumed to be H2 at 100 K average temperature, and an average pressure of 5 atm behind the shock, which gives a gas density of 1.2 kg/m3. This density implies a mass flow rate of dm/dt = 4 x 10-5 kg/s and since the pellet mass is 4 x 10-6, the lifetime of the pellet will be on the order of 100 ms based on the gas flow at the edge of the pellet. More gas is added from ablation along the sides, leading to a 40 ms pellet lifetime estimation without including liquid entrainment.
Solid H2 Pellet Ablation Experiments. Pellet injection experiments were performed at Prof. K. Kim's laboratory at the University of Illinois, Champaign. The injected solid H2 pellets were cylinders 3.2 mm in diameter and 6 mm long. They were initially at a temperature of 6-8 K and exited the acceleration apparatus at a speed of approximately 1 km/s. The pellets were injected into an inert gas and imaged through a window to examine pellet ablation.
Pellet Injector. High-speed injection of frozen pellets of H2 isotopes is used to fueling magnetically confined plasmas for controlled thermonuclear fusion research. [10] A basic single-stage gas-pulse gun was used here for pellet injection. The pellet-forming or freezing cell is located at the center of a liquid He-cooled cryostat. Heaters near the freezing cell are used to maintain the temperature of the breech and barrel above the melting point of the H2.
Since the pellet injector operates in an atmosphere of low pressure of He, the primary problem in using it for ablation studies has been to transfer the pellet to the pressurized test chamber without pressurizing the injector itself, which would lead to warm up and no further pellet production. The H2 pellets are frozen and fired at 5 - 9 K using 1000-1200 psi of driving gas. For these experiments the ablation chamber was pressurized using a fast gas valve. Injection was performed in N2 to avoid combustion.
Ablation Experimental Conditions. Pellet injection experiments were performed into vacuum, He, and N2. The specific fill method used has another important effect on pellet ablation: cooling the ablation gas. The gas flowing into the ablation chamber from the reservoir will expand isentropically from a high pressure to a low pressure and cool itself in the process. This is a major effect for expansion into vacuum. For a typical condition of 400 psi as the reservoir pressure, the final gas would exits the fill valve at 92 K for N2 (at 0.43 atm), and 78 K for He (at 0.87 atm) for an isentropic flow. This effect creates a cold gas environment in the ablation chamber, and it also creates a temperature gradient - the first gas in is colder than the last gas in. The overall effect is difficult to predict as a result of wall heating of the gas and because the first gas in is also heated to some extent by being compressed by the later gas.
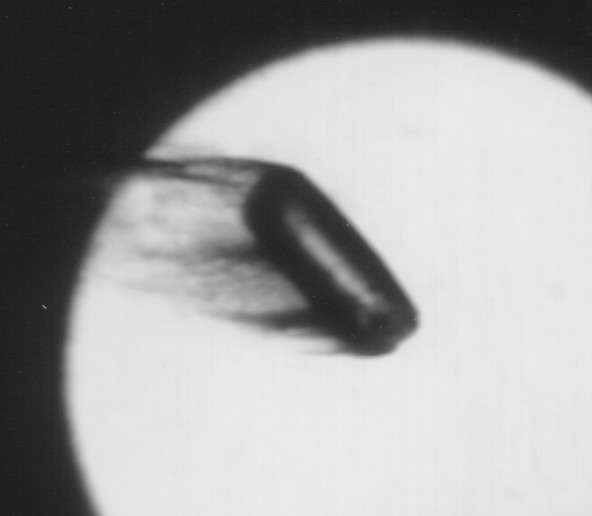
Figure 2. Image of pellet injected into a pressure of 0.32 atm of N2 79 cm from their entry into the ablation chamber.
Ablation Image Interpretation.The data from the ablation experiments is in the form of instantaneous images of the pellets as they are in the process of passing through the gas. The imaging system is nominally the same for all of the data. There is only one system, which has been moved between imaging stations at 17 cm and 79 cm from the end of the injector tube. Each image is of a different pellet. The pellets and pellet speeds are nominally the same.
There were four sets of image data: 1) Injected pellets just emerging from the injection tube, 2) Injection into vacuum, 3) Injection into He, and 4) Injection into N2 at 2 locations. Injection into both N2 and He was attempted to determine if gas condensation in front of the pellet is a controlling factor for the ablation rate. Images of pellets injected into vacuum at 17 cm from the entry point show the basic shape of the pellet, seen as a right circular cylinder with fairly flat ends. All images are consistent with this shape. The pellets are also consistently tumbling, presenting different perspectives of each pellet in each image.
As the pressure increases 50% and then 100% from the lowest pressure, the ablation appears to increase by at least those factors. Figure 2 shows significant pellet ablation at 0.32 atm in N2 (none were taken at 0.43 atm). Ablation is strongly dependent on fill pressure, although this difference in fill pressure may have caused a temperature difference as will as a pressure difference in the ablation chamber. For pellets injected into He the liquid shedding is greatly reduced.
Ablation Assessment The Mach # of the pellet must first be evaluated, since all of the shock parameters depend only on M. The pellet velocity is 1 km/s, but the speed of sound, a, depends on the gas temperature. The speed of sound in N2 at 300 K is 353 m/s. At the same temperature, the speed of sound in He is a factor of 2.9 times that of N2. If the ablation gas were at room temperature, the pellet would have M = 2.8 in N2 and approximately 1 in He. For the flow-cooled gases with a temperature of 150 K as discussed above the mach numbers are 4 for N2 and 1.4 for He.
Based on these mach numbers the parameters behind a normal shock can be calculated. For a M = 4 N2 flow the density ratio, ρ r, across the shock is 4.6 and the temperature ratio, Tr, is 4.0. For He at M = 1.5, ρ r is 1.7 and the temperature ratio, Tr, is 1.5. Since the pressure of the N2 in the ablation chamber is about half that of the He, and the density of He is 1/7 that of N2, the density of the N2 at the nose of the pellet is 9.5 times that of the He. The relative gas enthalpy is the ratio of ρ cpT for each gas; the specific heat of He is 5 times that of N2. This implies that the N2 has 5 times the enthalpy behind the shock as does the He. Balancing this heat source and the heat source of N2 condensation is the fact that the thermal conductivity of He gas is 5.4 times that of N2. The thermal diffusivities of the two gases are approximately the same, so the time to heat the pellet should be about the same.
The data shows much more ablation for the N2 than the He, even though the N2 pressures are half that of the He. One explanation of this difference would be the condensation heat release of the N2. The above argument tends to indicate that this is the case but the larger enthalpy of the N2 may also be the cause. Furthermore the Reynolds numbers in N2 are a factor of 7 higher than He, leading to greater heat transfer.
There is no evidence of a shock in any of the images. The shock standoff distance in front of the pellet at 1 atm is only 0.3 mm at Mach 3 so it would expected to be below the resolution of the imaging for a pellet with a spherical nose.
The tumble probably has a significant effect on whether the edges of the pellet are rounded as a result of ablation. For a pressure of 5 atm on one end of the pellet but not the other, that end of the pellet will undergo an acceleration on the order of 3 x 106 m/s2, which implies movement of a distance on the order of 1 cm in 0.1 ms. This implies that the pellets tumble rapidly if they are at an angle to the flow. The case where the pellets present their side to the flow is much more dynamically stable, as is the case usually seen. Rounding of the edges of the pellet can be used to derive an ablation rate and heating rate. Assuming an ablation rate of about 0.3 mm in 0.5 ms implies a regression rate of 0.6 m/s, which would imply that the lifetime of a 1 mm spherical particle would be on the order of 1 ms. This is probable an underestimate as a result of high heat transfer at the edges of the pellet. This implies a heat flux on the order of 107 W/m2, which is consistent with ablation modeling of a spherical particle that predicts a minimum heat transfer rate on the order of 106 W/m2, even at the reduced temperatures and densities of these experiments. Ablation is obviously present, and is much greater for injection into N2 as compared with He.
One very interesting aspect of the images with respect to H2 mixing is that the liquid H2 in the pellet wake always disappears within a distance of one pellet diameter or less. This is very rapid vaporization, and is consistent with high heat transfer to very small droplets. It also implies that mixing of the free stream gas with the H2 is primarily gas phase mixing of the wake. There is no question, however, that liquid shedding is a major phenomenon in solid H2 ablation.
Conclusions
The fundamental requirement for solid H2 scramjet fuelling is that the injected particles must be distributed across the combustor and fully ablate and mix during their residence time in the combustor. This work demonstrated that 1) Liquid jet injection of q = 6 injection is necessary for the jet to penetrate the flow. 2) A solid H2 jet with q = 6 and M = 3 flow (in the combustor at altitude) must have an injection velocity on the order of 100 m/s. 3) A 10 m long, 1 m wide, scramjet combustor operating at M = 3 (flight M = 9) will have a combustor flow residence time on the order of 10 ms. 4) A solid H2 particle must have a diameter of at least 1 mm in order for it not to lose so much of its 100 m/s cross-flow velocity that it will not travel the 1 m across the combustor in the minimum 10 ms residence time. 5) Modeling of the fluid mechanics of solid H2 particle ablation indicate a minimum heat flux to the liquid surface for vaporization on the order of 106 W/m2. 6) A vaporizing heat flux of 106 W/m2 results in a 10 ms ablation time for a 1 mm diameter H2 particle. Ablation due to liquid shedding would decrease this time significantly. 7) Given this minimum ablation time, the particle size and injection velocity can be adjusted to achieve the desired penetration and dispersion of fuel within the combustor. 8) Mixing will be extremely rapid as a result of wake mixing behind a host of small particles and extremely volatile and small liquid H2 droplets (demonstrated experimentally). 9) Ablation experiments indicate a particle lifetime of significantly less than 10 ms in a combustor.
Acknowledgements
Thoughtventions is grateful to NASA MSFC for its funding of this project under Contract No. NAS8-40546, and Prof. J. Schetz for his consulting aid.
References
1. S.C. Bates, "Technique for High Mixing Rate, Low Loss Supersonic Combustion with Solid Hydrogen and Liquid Helium Fuel," US Patent #6003300, 1999.
2. D. Less, and J. Schetz, "Penetration and Breakup of Slurry Jets in a Supersonic Stream," AIAA J., Vol. 21, July 1983, pp. 1045-1046.
3. A. Nejad, and J. Schetz, "Effects of Properties and Location in the Plume on Droplet Diameter for Injection in a Supersonic Stream," AIAA Journal, Vol. 21, July 1983, pp. 956-961.
4. "Performance Enhancement for Hypervelocity Airbreathing Propulsion, Workshop NASA Langley Research Center, Hampton, VA, July 29-31, (1991).
5. D.E. Daney, P.R. Ludtke, and C.F. Sindt, "Slush Hydrogen Pumping Characteristics Using a Centrifugal-Type Pump," in: Advances in Cryogenic Eng., Vol. 14, Plenum Press, NY, 438-445, (1969).
6. G.A. Cook and R.F. Dwyer, "Fluid Hydrogen Slush - A Review," in: Advances in Cryogenic Engineering, Vol. 11, Plenum Press, NY, 202, (1966).
7. Proceedings of the High Energy Density Matter Contractor's Conference, P.C. Carrick, 4-7 June 1995, Woods Hole, Jan. (1996).
8. S.C. Bates, "Prototype Cryogenic Solid Hydrogen Storage and Pellet Injection System," SBIR Phase I Final Report, USAF Phillips Lab Contract # F04611-93-C-0086, Report # PL-TR-94-3015, (1994).
9. W.H. Dorrance, Viscous Hypersonic Flow, McGraw-Hill, New York, NY, (1962).
10. S.L. Milora, "Review of hydrogen pellet injection technology for plasma fueling applications," J.Vac. Sci. Technol. A 7, 3, 925-37 (1989).