Magnetohydrodynamic Instability with Neutral-Beam Heating in the ISX-B Tokamak
J. L. Dunlap, B. A. Carreras, V. K. Paré, J. A. Holmes, S. C. Bates, J. D. Bell, H. R. Hicks, V. E. Lynch, and A. P. Navarro
Oak Ridge National Laboratory, Oak Ridge, Tennessee 37830
Abstract
This paper describes observations of magnetohydrodynamic instability with neutral-beam heating in the ISX-B tokamak and the theory specifically developed to support these experiments. The observed magnetohydrodynamic activity is explained by the resistive model presented but is not responsible for the observed degradation of confinement. Increasingly important n > 1 pressure-driven modes are predicted by the theory for the higher experimental βp values, but there is no experimental verification of their presence.
The ISX-B tokamak operates with up to 2.5-MW auxiliary heating power (total) from two coinjected neutral beams. Confinement degrades with increasing beam power (Pb), and the quantity βp√Ip "saturates" as a function of Pb, where βp denotes the volume-averaged poloidal β and Ip denotes the discharge current. Maximum volume-averaged total β obtained to date is ≈ 2.5%, well below values expected by extrapolation from results at low Pb. Descriptions of the device and of most other features of the neutral-beam experiments are available elsewhere.1-4
Our observations of magnetohydrodynamic (MHD) instability have covered the wide range of plasma parameters involved in these neutral-beam experiments. In this Letter, we describe these observations and the theory specifically developed to support these high-β experiments. We arrive at mode identification and consider the role of this instability in the degradation of confinement. These issues are important because tokamak operation has only recently reached plasma regimes with such β values, and the limitation observed here causes concern about the viability of the tokamak as a reactor concept.
Mirnov coils and collimated soft-x-ray detectors were used for instability diagnostics. The coils were arranged in arrays to determine the dominant poloidal and toroidal mode numbers (m, n) of the poloidal field fluctuations Bp in the shadow of limiters. The x-ray studies mainly used detectors in a 32-unit fan array centered on the outside equatorial and in a 24-unit fan array centered on the top vertical center line in the same poloidal section. Even during operation with maximum bandwidths (≈ 125 kHz), instability signals from all diagnostic channels were dominated by frequencies in the 5- to 25-kHz range. Data acquisition was both oscillographic and digital, the latter by a 56-channel CAMAC system.
Ohmically heated (OH) discharges suitable for injection heating in ISX-B are sawtoothing ones.5 Very low beam powers affect instability only by enhancing the amplitude and period of this classic sawtooth behavior. The instability signals are altered when the ratio of Pb to Ohmic power POH exceeds ≈ 1. The changes are first marked by a longer interval of m = 1 activity before internal disruption and the simultaneous appearance of strong Bp at the same frequency as the m = 1. Thereafter, the envelopes of X and Bp, where X is the fluctuating level of the x-ray signal, vary with plasma parameters. Generally, further increases in beam power lead first to longer-lived, even steadily running precursors and then to increasing amplitude modulation of these signals. Under some conditions the appearance of a long-period sawtooth is retained; in other cases it is not. This description strictly applies only to edge qψ ≤ 4.5, since patterns revert toward those of the classic sawtooth as qψ is increased.
Despite the variation of signal patterns with plasma parameters, the basic features of these signals do not change once the threshold Pb/POH ≈ 1 is passed. The Bp at the Mirnov coils is strong, often exceeding Bp/Bp = 1% at major radius R ≈ R0 + 0.3 m near the outside equatorial, where (m = 2, n = 1) mode symmetry is dominant. From Bp, mode rotation is the reverse of that in OH plasmas, possibly because of toroidal rotation driven by the coinjected neutral beams.6 The large X signals are from within q ≈ 1 and are due to a large m = 1 mode there. Rotation of this m = 1 structure is also reversed. Despite the large (m = 2)/(n = 1) Bp, there is no large or distinctive X from near q = 2 and thus there can be only a small 2/1 island structure. The X wave forms show significant differences of detail when compared with the work of others7 on the classic m = 1.
The JFT-2 tokamak yields somewhat similar instability signals when operated with neutral-beam heating at β values like those of ISX-B.8 Not enough details from JFT-2 are available for a definite conclusion, but it appears that the same basic instability is present in both devices.
The stability properties of ISX-B-like plasmas have been studied in the framework of the resistive MHD model,9 a nonlinear, three-dimentional model expressed by a reduced set of resistive MHD equations valid in the limits of large aspect ratio (ε = a/R << 1) and high β (β ~ ε).10 The equilibria were obtained by solving the Grad-Shafranov equation (exact to all orders in ε) in a flux-conserving manner. For systematic theoretical studies, the equilibria were characterized by a pressure profile p = p0ψ2, a safety factor (q) profile, and the shape of the outermost flux surface. Several sequences of equilibria were studied.9 They gave the same qualitative results. At low βp, the most unstable mode is the n = 1. Its linear stability properties with increasing βp are summarized in Fig. 1. At low β and in the cylindrical limit, this mode is just the (m = 1; n = 1) tearing mode. With increasing pressure, the mode goes from the tearing branch to a pressure-driven branch. Higher-n modes become linearly unstable with increasing βp; they are essentially pressure driven and have ballooning character.11 All of these results are for equilibria stable to ideal modes.
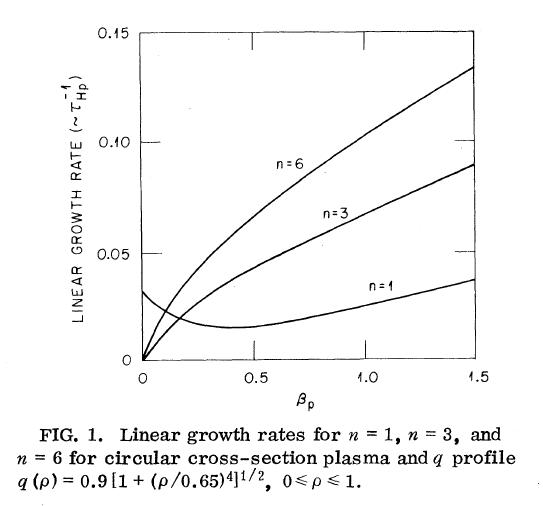
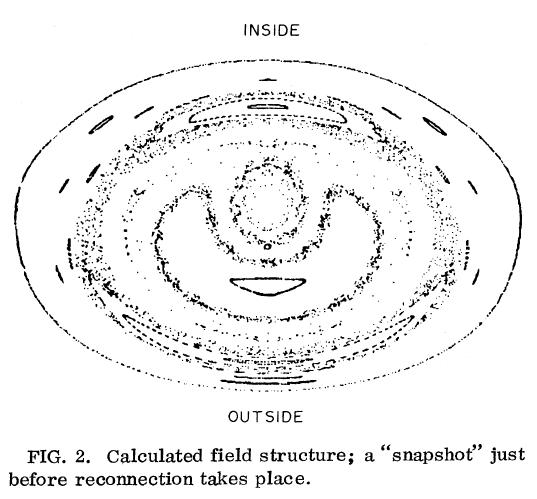
For the lower range of βp values obtained with beam heating in ISX-B (βp < 1), the theory shows an instability that is best described as a βp distortion of the (m = 1; n = 1) mode. This mode drives many other helicities through the toroidal and nonlinear couplings. The man results the toroidal and nonlinear couplings. The main results are as follows: (1) For a given q profile, growth of the m = 1 island slows down with increasing βp, from exponential to linear, before reconnection takes place. (2) If βp is high enough, the island saturates without reconnection and therefore produces continuous m = 1 mode activity. This happens when the (m = 1; n = 1) mode is primarily driven by pressure. (3) The largest driven mode is the (m = 2; n = 1). This component, like the other driven modes, is mainly localized near the q = 1 surface. It produces a large Bp at the limiter but only small 2/1 islands near q = 2 and hence only small X. (4) A broad spectrum of other driven modes is produced. These generate a variety of magnetic islands that often overlap and break magnetic surfaces (Fig. 2). (5) As the edge q is raised, the instability reverts toward the classical low-β m = 1.12 Growth of the m = 1 island speeds up as a result of increasing shear at the q = 1 surface, and the amplitudes of the driven modes and Bp at the limiter decrease because the radius of the q = 1 is reduced.
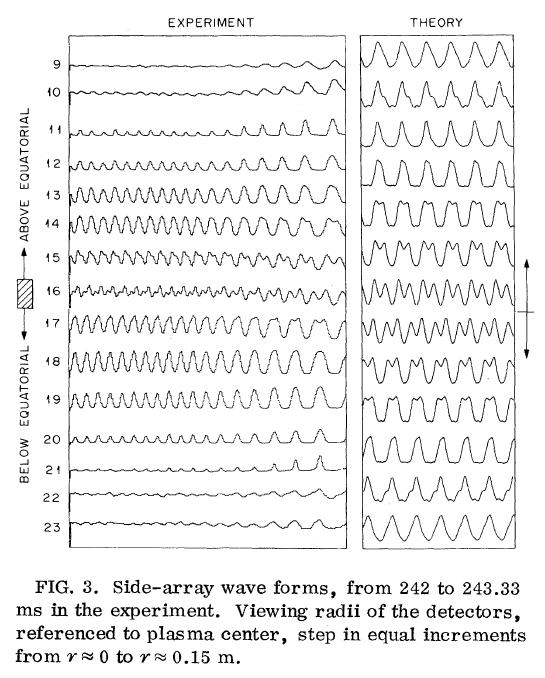
These theoretical results and the gross features of the experimental observation are clearly in agreement. A comparison at a more detailed level is done by using equilibria reconstructed from laser-profile and magnetic data and calculating X wave forms from the theoretically predicted mode structure. In this procedure, X along various chords was calculated as a line integral of p2, and toroidal rotation of the mode structure at a constant frequency ω was assumed. Figure 3 is a comparison of experimental and theoretically derived wave forms for the side-mounted array. The theoretical ones resulted from corotation of the instability structure shown in Fig. 2. Features of a dominant m = 1 (Ref. 7) are evident in both displays. Additional fine-grained details are common to both: (1) The channel nearest center shows the expected dominant 2 ω resulting from the m = 1. Successive peaks on center are not of equal amplitude, a feature that in the model calculation results from the presence of the driven m = 2 rotation in phase with the m = 1. (2) The double humps on positive half cycles at nearby channels, e.g., 15 and 17, are also not equal and the ordering of the inequality reverses between upper and lower channels. These features are again the result of the m = 1 and m = 2 coupling. If counterrotation is assumed in the model, the theoretical traces for channels 15 an 17 are exchanged and then disagree with the experimental traces. (3) At channels 10 and 22, the wave forms are triangular in nature and are again reversed between upper and lower channels. This is just outside q = 1, where the (m = 1; n = 1) eigenfunction no longer dominates and so no longer obscures the effects of coherent superposition of all the other driven mode components. The assumption of counterrotation exchanges the theoretical traces and again leads to disagreement with the experimental ones.
As βp increases to the higher ranges obtained in ISX-B, the role of additional n > 1 modes in the overall predicted mode structure becomes increasingly important. Since these modes are linearly unstable, they are not linked to the evolution of the (m = 1; n = 1). At very low resistivity, these n > 1 modes saturate at small amplitude, but their overall level is large enough to potentially influence transport. At these values of resistivity and βp, the numerical calculations are very difficult and their study is not yet complete.
In this higher-βp regime, the experimental Bp and X wave forms continue to show the distorted (m = 1; n = 1) mode. They have not shown the presence of the additional incoherent n gt; 1, high-βp modes predicted by the theory. Because our diagnostics are signal-averaging in nature and may be restricted to too low frequencies, they may be insensitive to such highly structured modes.
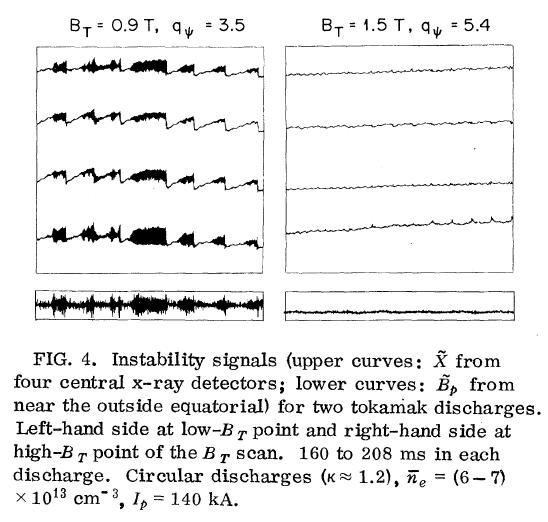
We have no positive experimental correlation between observed mode activity and the degradation of confinement with increasing Pb. Our best efforts have been toroidal field (BT) scans at fixed plasma current and density, which use the fact that raising edge q reduces the intensity of the m = 1 and driven modes and, presumably, any associated losses. Scans at Pb ≈ 2 MW yielded essentially constant βp despite marked changes in MHD intensity. With Pb reduced to 0.6 MW to produce a βp value out of saturation and a plasma regime in which the independently unstable, high-n, pressure-driven modes are less likely to be important, the amplitude of the instability signals again decreased markedly as BT was raised (Fig. 4). However, βp did not increase; neither did the stored energy (∝ βpIp2) or the gross confinement time (∝ βpIp/Pin).
We conclude that the MHD activity observed in ISX-B is well understood in terms of the resistive MHD model and that this observed activity is not responsible for pronounced degradation of confinement. The n > 1, pressure-driven modes predicted by the model are a possible explanation for the observed degradation, but their presence in this plasma has not been experimentally verified.
We acknowledge with appreciation the support of our many colleagues in the ISX-B group and in the engineering staff. This research was sponsored by the Office of Fusion Energy, U. S. Department of Energy, under Contract No. W-7405-eng-26 with the Union Carbide Corporation.
References
1. M. J. Saltmarsh, J. Vac. Sci. Technol. 17, 260 (1980).
2. M. Murakami et al., in Plasma Physics and Controlled Nuclear Fusion Research - 1980 (International Atomic Energy Agency, Vienna, 1981), Vol. I, p. 377.
3. D. W. Swain et al., "High Beta Injection Experiments on the ISX-B Tokamak," to be published.
4. E. A. Lazarus et al., in Proceedings of the Tenth European Conference on Controlled Fusion and Plasma Physics, Moscow, 14-19 September 1981 (to be published).
5. S. von Goeler, W. Stodiek, and N. R. Sauthoff, Phys. Rev. Lett. 33, 1201 (1974).
6. S. Suckwere, H. P. Eubank, R. J. Goldston, E. Hinnov, and N. R. Sauthoff, Phys. Rev. Lett. 43, 207 (1979).
7. N. R. Sauthoff, S. von Goeler, D. R. Eames, and W. Stodiek, in Proceedings of the International Atomic Energy Agency Symposium on Current Disruption in Toroidal Devices, Max-Planck-Institut für Plasmaphysik Report No. IPP 3/51, 1979 (unpublished), paper C-5.
8. S. Yamamoto et al., Nucl. Fusion 21, 993 (1981).
9. J. A. Holmes et. al., Oak Ridge National Laboratory Report No. ORNL/TM-8063, 1982 (unpublished).
10. H. R. Strauss, Phys. Fluids 20, 1354 (1977).
11. H. R. Hick et al., in Plasma Physics and Controlled Nuclear Fusion Research - 1980 (International Atomic Energy Agency, Vienna, 1981), Vol. I, p. 259.
12. G. L. Jahns et al., Nucl. Fusion 18, 609 (1978).