Stable High Concentration Matrix Isolation of High Energy Species
40 Nutmeg Lane
Glastonbury, CT 06033
Abstract
A number of cryostabilized additives (CSAs) isolated in solids have been created in the past, but not yet at concentrations high enough to have engineering value as propellants. The atomic scale physics of the sublimation concentration process are investigated to motivate an experimental investigation of this technique to achieve high density CSAs. Previous research has extensively investigated the high surface mobility on solid hydrogen surfaces and concluded that this phenomenon prevents the formation of high concentration CSAs. Removal of surface matrix atoms during the sublimation concentration appears to provide a means for removing this mobile layer, allowing CSA concentration. Modeling has been done to estimate approximate concentration limits as a function of reaction distance and reaction energy release. The sublimation concentration technique is further refined for creating high volume densities of a CSA in solid para-hydrogen.
Nomenclature
| A | = Angstrom |
| D | = Diffusion constant |
| dr | = Reaction distance |
| E | = Energy |
| H2 | = Hydrogen |
| hcp | = Hexagonal close packed |
| Isp | = Specific Impulse |
| J | = Joules |
| k | = Boltzmann's constant |
| K | = Kelvins |
| Li | = Lithium |
| M | = Gram-molecular weight |
| T | = Temperature |
I. Introduction
Matrix isolation of high energy species1 has been performed for many years, but only low overall stable concentrations have been achieved experimentally2. The inclusion of even moderate concentrations of such species in a standard propellant would provide a new chemical propellant with a revolutionary improvement in specific impulse3. Although the energetic species may be molecular or atomic, for simplicity of description, they will here be assumed to be atomic. There are two reasons for the low concentration limits of doped cryogen solids that have been experimentally achieved to date: species reactivity and processing limitations. The former is fundamental, whereas this work pursues processing routes that attempt to avoid the processing limitations of past work to achieve high cryostabilized additive (CSA) concentrations.
Modeling predicts that CSAs can exist at a relatively high concentration in a stabilizing inert matrix. The highest theoretically achievable concentrations are predicted for substitutional CSAs evenly distributed throughout a perfect crystal lattice. Experimentally achieved CSA concentrations are far below these predicted limits. Possible explanations for the low experimental concentrations include the diffusional effects of lattice imperfections and global instabilities resulting from random local CSA concentration fluctuations. Although neither of these effects have been studied in detail, it appears unlikely that either of these mechanisms explain the very large differences between predicted stability and experimental demonstration. It is difficult to quantify this argument due to the varying modeling assumptions and experimental constraints, but modeling predicts stability on the order of 10% atom concentration, whereas experimentally only 0.1% concentrations have been achieved.
The limiting factor appears to be the process by which the CSA-doped matrices are formed. Random concentration fluctuations and mixing in the accretion layer as the solid forms seem to cause the much lower CSA concentration limits found experimentally. This situation is exacerbated by the existence of a highly mobile layer on the surface of solid H2 crystals that allows liquid-like reaction conditions. It may be possible to deposit CSAs at low concentration, and then remove matrix material to increase the stable CSA concentration, as is proposed in the present study, by subliming the matrix. The goal of this work is to study whether useful (in an engineering sense) concentrations of CSAs can be expected to be created experimentally, based on an understanding and modeling of the physics of the sublimation concentration process.
II. CSA Concentration Limitations
The reactivity of CSA atoms results in fundamental limitations on achievable overall CSA concentrations, primarily due to spatial constraints on the distribution of the atoms. When two reactive atoms come into close enough spatial proximity, the attractive forces between the atoms can destabilize the local matrix atomic structure (solid or liquid) and pull the atoms together through the matrix molecules so that reaction occurs. The thermal energy release from any local reaction destabilizes the surrounding crystal matrix further, causing/enabling reaction of other nearby reactive atoms, the energy from which, in turn, leads to global instability and often explosive reaction. The minimum stable distance between CSA atoms, which will be termed the reaction distance, dr, is therefore a critical parameter, as are the parameters that control this distance.
The reaction distance is determined by a balance between the stabilizing lattice strength and the forces between CSA atoms, described in detail by the three-dimensional potential energy surface in which the two atoms reside (e.g. 4,5). The net force between the two atoms is a vector property, since crystal forces are inherently not spherically symmetric, and it is not simply defined by the two reacting CSA atoms in the host matrix, but is a result of the field of CSA atoms in the crystal.
For a substitutional CSA with a spherically symmetric zero reaction energy barrier in a hcp crystal, CSA atoms cannot be nearest neighbors. For a short enough reaction distance length, alternating CSA and matrix atoms is a theoretically stable configuration, implying a 50% concentration limit. Such a limit might possibly be reached in the experimental case of epitaxial deposition, a strong enough matrix, and weak enough forces between the CSA atoms. It should be further noted that a uniform 3-dimensional array of CSA atoms will tend to stabilize the overall matrix and increase the effective dr, since each CSA exists in a balanced force field among the other CSAs rather than experiencing directed force from a single nearby CSA atom. Thus, above some minimum CSA concentration level, stable concentrations should be significantly higher than those predicted by two-atom stability calculations.
Normal and necessary concentration fluctuations that arise from gaseous deposition to form a solid mean that stable, deposited atom concentrations must be low enough that the extreme of the atom positions does not result in destabilizing reaction. Thus, achievable real average concentrations are much smaller than would be the case if the atoms could somehow be evenly dispersed throughout the volume.
The second primary limit on maximum CSA concentration arises from the process by which the CSA is formed. The doped solid matrix must be formed via a high mobility accretion layer where the CSA is frozen into a solid state mixed with the carrier material. Direct freezing without a liquid layer leads to a porous solid6. Within the accretion layer random motion of the reactive atoms can cause them to come within reaction distance as they condense, leading to much larger effective reaction distances and much lower stable concentrations compared with the solid. This situation is further complicated for a primary matrix candidate, H2, which, even as a solid, possesses a mobile surface layer7.
III. The Accretion Process
It is highly probable that a practical CSA propellant must be formed by creating the CSA in the gas or plasma phase by some energetic process, followed by co-condensing the gaseous CSA with a gaseous matrix material to form a solid mixture. The transition from gas to solid must occur in some continuous process in a layer on the surface of the cryogenic solid. This layer moves in space as the solid is built up, with continuous addition of gaseous hotter material on one side, and solidification combined with heat transfer on the other side. Usually this accretion layer forms a continuous liquid layer, but at low energy deposition rates the gas mixtures can condense directly into a solid.
The maximum stable concentration of a CSA in a liquid is much lower than in a solid first because the resistance of the material separating the CSA atoms is much less than in a solid, and second due to local and larger scale motion in the liquid. Thus, in the accretion layer there is an effective reaction distance, deffr, that is much larger that dr in the solid; how much larger depends on the temperature, density, and viscosity of the liquid, the depth of the layer, and the speed of the solidification front in the limit of very low concentrations.
The track of deposited atoms in the accretion layer is yet another concentration limiting effect. The CSA atoms generally impact the accretion layer with considerable momentum, causing them to penetrate the layer to a significant depth. If, during the penetration, the path intersects the location of another CSA atom, reaction will occur. Furthermore, if the path penetrates the solid, it will tend to liquefy a cylindrical volume around the path, and this, too, can lead to reactions that might otherwise not occur. This is an important problem with laser ablation deposition.
Irrespective of the reaction-inducing mechanisms and their limiting effects, it seems clear that the accretion layer should be minimized to achieve maximum CSA concentration. This can be done by precooling the CSA gas to the maximum extent possible before deposition. Unfortunately, totally eliminating the accretion layer does not appear to be practical because direct solidification from the gas leads to porous crystals; various techniques are available for creating high quality H2 crystals6.
In the past thermal sources1, and, more recently, laser ablation sources (e.g. 2) have supplied the energetic species. Neither of these schemes seems appropriate to maximize CSA concentration. CSA atoms carried to the deposition surface in cold He gas is a much more promising approach.
IV. The Mobile Surface on Solid H2
Most experiments that have been performed to concentrate a CSA for propellant use have used solid (para) H2 as the inert matrix. This choice was made both because H2 is a relatively stable fuel with a high Isp (although poor volume efficiency) and because the very low temperature at which the solid forms (14 K) leads to a great deal of added thermal stability. Hydrogen, however, forms a quantum solid that has some very unusual and important properties for the purposes of forming a high concentration CSA mixture. Specifically, even as a solid, there is a highly mobile surface layer on solid H2. The topmost layers appear to remain fluid as temperatures decrease to far below the critical temperature of H27.
Research on this mobile surface layer is important both because it is believed to be the fundamental limitation that prevents the formation of high concentration CSA mixtures required for propellant preparation.
At this time the existence of a mobile layer on solid H2 has been well established through a number of experimental studies. In 1992, Albrecht et. al.7 reported wetting phenomena studies on solid H2 using the surface plasmon (SP) resonance technique (ATR; attenuated total reflection method), which provides accurate information about both the thickness and the roughness of the physisorbed material. Using condensation from H2 gas it was found that the deposited film is smooth up to a thickness around of 12 A. This dependence was interpreted as the build-up of a smooth, homogeneous mobile film up to a limiting thickness d1 of 3 to 4 monolayers, beyond which the condensing molecules aggregate to form bulk crystallites.
Their analysis yielded an Arrhenius-like behavior, ∝ exp(-ΔE/kT) where ΔE ≅ 23 K7 for the case of H2, and the energy ΔE can be associated with the activation energy for surface diffusion. The activation energy for bulk diffusion is so high that this mechanism is negligible in the temperature range considered here. No dependence on ortho/para-concentration was found.
Further experimental work was done to explore the behavior of the mobile surface film using a hole burning technique8. This work evaporates a well of H2 above a heater element, measuring the filling of this well by reevaporation after varying intervals. The driving force being the attractive forces of stronger binding to the substrate for deeper layers. They found the surface diffusion to have a diffusion constant of D0 = 2 x 10-4 m2/s +/- 10% with an activation energy of 43 K +/-15%. They posit a surface in equilibrium with a two-dimensional vapor above the surface, and that this vapor provides a diffusion mechanism. Apparently the effects of the mobile H2 surface layer are very similar to the accretion layer during freezing.
Doped H2 crystal growth at temperatures above about 3 K is thus subject to the concentration-limiting effects of this mobile layer. Hardly any experimental studies previous to the discovery of the mobile film were done at this low temperature; this appears to be the CSA doped concentration limiting process.
It is believed that continuous sublimation removes this surface mobile layer; this is certainly true if the mobile layer results from a vapor equilibrium effect. This has the major practical implication that sublimation concentration can take place at much higher temperatures, making it a much more rapid and practical process.
V. Sublimation Concentration Process
Both previous modeling studies (e.g.9) of doped matrix stability and accepted solid diffusion coefficients imply that much higher concentrations of energetic species are stable in a solid cryogenic matrix compared with what has been experimentally demonstrated to date. Furthermore, concentration limitations associated not with the end state but with the processes used to reach this end state are consistent with the lower experimental concentration limits. It seems highly probable that higher stable energetic CSA atom concentrations could be achieved if some appropriate physical route to this goal could be found.
The problem then becomes how to create an experimental process that can approach the theoretically achievable concentrations. The process investigated here is first to form the solid at low enough concentration such that negligible reaction occurs during a standard and established formation process, and then remove matrix material by sublimation to concentrate the energetic species. Low concentration doped matrix formation has been done many times; concentrating the energetic species in the solid not yet been attempted experimentally. The author has proposed sublimation concentration in previous work10,11, examining the general properties of cryostable additives, and the specific engineering and scientific techniques and motivation for sublimation concentration. One advantage of using a low concentration starting state is that the crystal can be annealed to eliminate defects.
Sublimation concentration is fundamentally a stable process because 1) the energetic species is always trapped within the solid matrix at extremely low temperature, essentially eliminating diffusive motion or relative motion in a mobile surface layer, 2) during the process, the mobile H2 surface layer is removed by the continuing sublimation, so that the surface is stable, and 3) the energy release from any reactions that might occur due to low probability adjacent reactive atoms is absorbed by the sublimation. Together, these factors should allow concentration of energetic species at the solid matrix surface by at least a factor of 10 beyond past practice. By creating multiple concentrated layers, one can prepare engineering quantities of a high energy species CSA propellant.
The primary goal of the physics investigation described here is to determine what the concentration limits are on the sublimation process, and which specific physical phenomenon is the limiting factor. One would expect the sublimation concentration limit to be much higher than achieved in the past; an important question is whether the limits are high enough to warrant experimental investigation.
The basic physical processes of sublimation concentration are 1) removal of H2 molecules from the surface of a H2 solid that has widely dispersed CSA atoms substituted for H2s at random locations, 2) removal of H2 molecules from the surface of a H2 solid nearby and adjacent to a CSA atom, 3) expulsion/removal of H2 molecules and reacted CSA dimers as a result of CSA atom recombination during sublimation, and 4) Motion of the CSA atoms during the sublimation process.
VI. Sublimation Modeling
The starting state of the sublimation concentration process has been simulated mathematically by creating a random distribution of points in a three dimensional volume, where each point represents an energetic atom, in a surrounding space filled with matrix molecules. Shown in Fig. 1 is a two dimensional map of 1000 points (energetic atoms). The points are distributed randomly in the x, y, and depth dimensions. For a specified number of points the depth dimension and the diameter of the space-filling matrix atoms control the volume concentration; the figure shows a top view projection of the 3-dimensional atom distribution. The randomness of the distribution is visually evident in the figure and becomes more evident as the number of points is increased.
Figure 1. Random two-dimensional distribution of 1000 points in a grid.
Shown in Fig. 2 is the identical distribution as seen in Fig. 1, where the red-circled crosses identify all points that are within a specified distance of another point - CSA atoms that are close enough to react. The case shown in the figure is for a distance constant of 0.010 in the arbitrary units. There are 246 close points in this case. The fact that the circles mark the close points and all of the close points was checked by magnifying different locations on the grid and measuring the pair separation. Visually it is easy to identify close pairs, mathematically it is quite difficult without very large calculations. At the same time it can be seen that there are significant areas with few or no points at all.
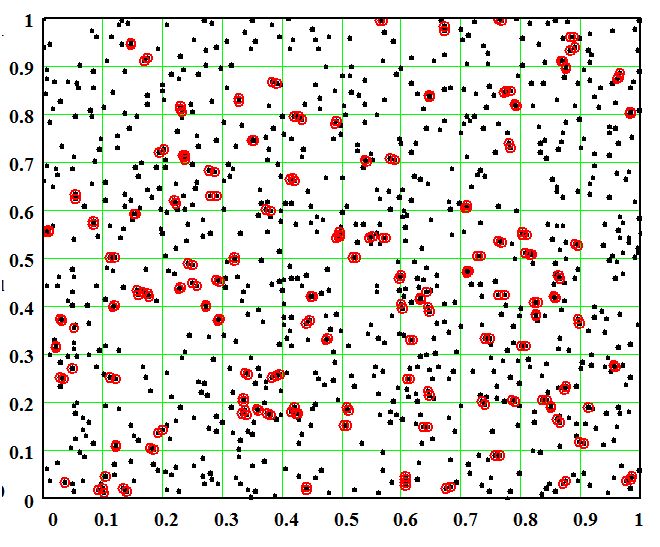
Figure 2. Random two-dimensional distribution of 1000 points in a grid, identical to Fig. 1 with points separated by 0.01 identified by red circles.
It is evident from Fig. 2 that the close points are distributed randomly. The number of close points is an important feature of the model. Figure 3 shows the number of close points as a function of the separation distance parameter dr. The number of close points increases by a function that is less than a square of the separation up to some saturation level where the dependence becomes linear. The model indicates that 50% of the points are close to another point if the separation parameter is approximately 0.015 - 1.5% of the overall scale of the overall length scale of the point distribution area.
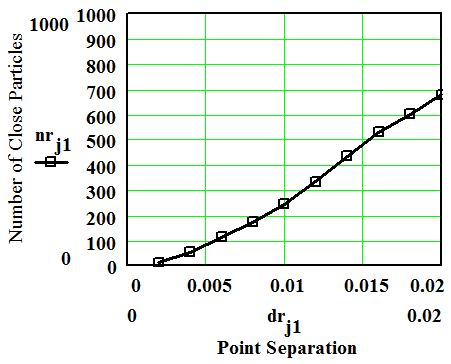
Figure 3. Number of close points as a function of maximum point separation.
VII. Modeling Implications for the Sublimation Concentration Process
The initial state for the model was chosen to be/represent a random field of 1000 CSA atoms immersed in a matrix of 106 host molecules, representing a concentration of 0.1 % CSA atoms. This concentration was chosen because a 0.1% atom matrix deposition has been achieved experimentally and is a reasonable practical starting point for a real concentration process. The volume of the mathematical process space is 1 x 1 x 0.1 arbitrary units, so that for 106 hcp molecules, the molecular diameter would be approximately 0.0045 units. Shrinking the depth dimension to a single-layer surface dimension would then simulate concentrating the CSA atoms using sublimation by approximately a factor of 20. A way to visualize the packing is to think of a 105 atom volume as 100 x 100 x 10 deep. However, it has been realized through this modeling work that the depth and volume concentration is immaterial; the volume is collapsed onto a surface, the only difference for a greater depth is that the sublimation takes longer; all of the CSA atoms end up on the surface.
The sublimation process consists of removing matrix H2s, where isolated CSA atoms do not sublime due to their higher molecular weight, and thus all of the CSA atoms migrate from the mixture volume into a surface layer. The points shown in Fig. 1 then represent both a top view of the initial CSA atom volume distribution and also the approximate result of sublimation concentration where the CSA atoms below the surface are brought to the surface by the sublimation of the H2s - without reaction. This assumes that the CSA atoms only move vertically, or that lateral motion averages out and does not change the essential random distribution of CSA atoms. Assuming a perfect hcp crystal, the effective CSA concentration in a matrix can be changed by maintaining the same CSA spatial distribution while varying the hcp space-filling diameter of the matrix atom. This simulation breaks down for very high concentrations, where the CSA atom location must be at discrete substitutional lattice sites.
The in-plane surface distance (x -y distance) between all pairs of CSA atoms can then be used to determine how many pairs are close enough to be able to react; their separation is less than some threshold value for reaction. The reaction distance is the maximum distance between CSA atoms in the H2 matrix where the CSA atoms will draw together through the matrix atoms and react. In the real case this distance is a complex, three-dimensional determined by the crystal potential energy surface, but for the model described in this paper an average is used. The reaction distance, dr, is measured in terms of the molecular diameters of the matrix material, which makes physical sense, since the impeding forces to the attractive forces between the CSA atoms are a function of the number of matrix atoms intervening between the CSA atoms. In the real case dr will be a quantum function depending on the center distance between CSA atoms and their relative positions in the lattice.
The reaction of two CSA atoms results the creation of an excited dimer, where the excitation is in the form of vibrational and rotational energy. The dimer is at the surface, and must either leave the surface or lose its energy to surrounding H2 molecules. There seems to be little question about the fate of CSA atoms that react during the sublimation process: sublimation and removal from the surface. Clearly the reaction energy is much larger than the surface binding energy, so the excited dimer comes off the surface together with some number of H2 molecules.
As an example, the energy released when two lithium atoms to form a dimer is about 1.14 eV, or about 1.3 x 104 K. The sublimation energy of H2 is 89 K, and this must represent the order of magnitude of the binding energy of the reacted and energetic dimer to the surface. Since the released energy is so much greater than the binding energy, the dimer must sublime. It may cause some of the surrounding H2s to sublime also, but that will not affect the surface or process stability.
Another possibility is that the excited dimer reacts with an adjacent H2 molecule to release more energy. However it has been shown by dissociative excitation of O2 in H2 solids that the O atoms do not react with the H2 molecules12. During the solid formation process, CSA atom reactions occur within the volume where the reaction energy must be absorbed by the surrounding volume, causing instability. During the sublimation process the reactions always occur at the surface where the energy release simply expels the reactants into the surrounding vacuum.
The model as presently configured is an end state model that determines how many CSA atoms have come close enough to react after the sublimation concentration process is complete. The original goal was to find the ratio of atoms to dimers on the surface and then assess the concentration of these two species. The fact that the dimers sublime away without destabilizing the process implies a very different surface filling process. In this case, as an end state, the remaining CSA atoms would represent the final surface concentration. However, examining the sublimation, reaction, and dimer sublimation processes together, it becomes evident that as each pair of CSA atoms react, form a dimer, and sublime, a gap is left in the CSA atom pattern. This gap would be filled in by another CSA atom at a greater depth being sublimed to the surface, making a more uniform distribution of CSA atoms, and eliminating clusters. In the specific case shown in Fig. 2 clusters of 3 will be a single CSA atom at that location in the final state; triplets represent overcounting of the number of reacting atoms.
It is notable that the only limit to the amount of H2 that can be removed during the sublimation process is the time it takes. For a very thick sample containing a low concentration CSA atoms throughout, sublimation of the H2s will lead to progressive concentration until the loss of CSA atoms through reaction will balance those added to the surface by sublimation. This provides a method for starting with a random CSA distribution and ending with an evenly spaced, uniform distribution, since all of the gaps (see Fig. 1) resulting from randomness are eventually filled in, while close CSA atoms are removed from the surface by reaction and sublimation.
The critical point is that as the sublimation process proceeds, close CSA atoms are continually eliminated, while new CSAs atoms come to the surface and steadily fill in the spatial gaps that occur as a result of random deposition. Eventually some steady state is reached where every time a CSA atom approaches the surface it reacts with a CSA atom already on the surface to create a gap in the surface distribution. Further modeling will have to be done that includes the progression of CSA atoms to the surface to determine the final achievable concentration.
One of the more subtle questions about the sublimation process is the dependence of the sublimation rate on the progress of the progress. As the surface fills up with CSA atoms, the H2 sublimation rate will decrease, simply because the surface area of H2 is decreasing. This will increase the overall sublimation time and may provide a diagnostic of the progress of the process. A related effect is the necessity for some H2s to migrate from beneath CSA atoms, which should be limited by some combination of vacancy diffusion and H2 motion due to sublimation.
The surface geometry will be evolving as the sublimation process proceeds. It will certainly not be flat. Due to bond deficits or surpluses, protrusions will tend to be preferentially sublimed away more rapidly, while depressions will be sublimed more slowly, such that the overall sublimation process will tend to produce relatively flat final surfaces. Dimer reactions will tend to produce shallow craters in the surface, but the surface should stay relatively flat so that the surface geometry should not have a major overall effect on the process. There will be steps in the surface, and enhanced diffusion along the steps.
A. Solid Diffusion Effects.
Critical to the process is that the CSA atoms on the surface do not move rapidly and react. The mobile layer on solid H2 is removed by sublimation, but there remains the basic solid diffusion rate, enhanced by the lack of a total cage surrounding the CSA atoms because they are on the surface. It is argued that the thermal diffusion rate is slow enough to not affect the process at the temperatures at which the process takes place.
The diffusion rate of species within a cryogenic matrix or compound is not well known in general. Assuming the basic classical diffusion law D = D0exp(-ED/kBT), for self-diffusion, D0 values are estimated to be 3 x 10-3 for H2 and 4 x 10-4 for D, with activation energies ED/kB of about 200 K13 at zero pressure. This would imply D(4 K) = 6 x 10-25 cm2/s. Quantum diffusion dominates overall diffusion for the light species at temperatures below 6-7 K in H2 crystals. At higher temperatures thermally activated diffusion plays a dominant role. As a first approximation a quantum diffusion coefficient is proportional to temperature. At low temperatures quantum diffusion (tunneling) leads to much higher actual diffusion rates; D(H2) = 2 x 10-6e-112/T, so that D(H2, 4 K) = 1.4 x 10-18 cm2/s. The absolute numbers are very small; quantum diffusion is difficult to measure experimentally. As an example of this diffusion rate, for planar diffusion from 100% concentration into a semi-infinite body at 4 K, the concentration would reach 50% 1 nm away in 2 hours. At 2 K the quantum diffusion coefficient of H2 is close to 10-20 cm2/sec.
With respect to CSA atom diffusion, a heavier, but not necessarily larger (as measured by interaction potential) species than H2 is diffusing toward another of its kind as a result of attractive forces between the two CSA atoms. In a perfect lattice the atoms would have to plow through a mass of H2 molecules, and the diffusion rate would be expected to be much slower than the movement of light and small H2 molecules. However, diffusion in practical materials is strongly dependent on lattice imperfections - vacancies and a variety of structural imperfections. In the real case the diffusion mechanism is probably that a H2 crystal vacancy would migrate between the two atoms, driven by a decrease in overall crystal energy due to the atoms being able to move closer to each other. The atom would then move to fill the vacancy, making progress in the diffusion process. The next step would be more difficult, because the mechanism for the vacancy to diffuse again in front of the atom is more complex. A H2 molecule would have to tunnel through the atom, or a sequence of H2s would have to move around the atom to move the vacancy in front of the atom again to allow it to move another lattice step. This would be the rate limiting process, assuming a relatively low volume vacancy concentration. Vacancy concentration appears to be the dominant atom diffusion mechanism.
Vacancies in solid H2 are equilibrium lattice defects and their concentration is supposed to be unambiguously determined by temperature and pressure. According to various estimates, at the triple point (T = 13.81 K) of H2 the concentration of vacancies is from 0.1 - 0.01 %, decreasing rapidly with decreasing temperature. Dislocations and packing defects are the main defects in single crystals and polycrystalline samples (with respectively large grains) of pure H2. The maximum density of dislocations in para-H2 is on the order of 1010 cm-2, whereas in normal H2 it can be an order of magnitude higher. In well-annealed single crystals the density of dislocations can be decreased to values perhaps as low as 102 - 103 cm-2 14. One would thus expect diffusion in solid H2 to be strongly dependent on the history and preparation of the sample.
For the case of sublimation concentration, surface, not volume diffusion, is important. The CSA atoms will be embedded in the surface, but the diffusion constants will be significantly larger due to the decrease number of bonds at the surface. The number of surface bonds of the CSA atom will also be changing as H2 molecules sublime around it. Diffusivities are small, but this is a motivation to limit the time over which sublimation concentration takes place - the starting volume concentration should be as high as possible. The effect of surface diffusion is a question that will have to be answered experimentally.
B. Sublimation Concentration Limits
Clearly there is a final concentration limit associated with sublimation concentration. At some concentration the loss of CSA atoms through reaction will balance those added to the surface by sublimation. At this point the concentration fluctuations across the area will be small and the surface concentration relatively high, approaching the theoretical value for CSA atoms embedded in a surface.
If one takes Li as an example CSA atom, and assuming that the reaction limit is 2 atom diameters in a hcp lattice4, then there are 8 matrix atoms for every CSA atom as shown in Fig. 4, and the ideal concentration is 12.5% CSA concentration in the surface atoms. The remaining fluctuations in separation distance will probably decrease this to perhaps 8% in the real case, since a 2 atom separation is the minimum practical distance. It is not clear what the stabilizing effect of the entire atom field will be, but it will increase the stable concentration.
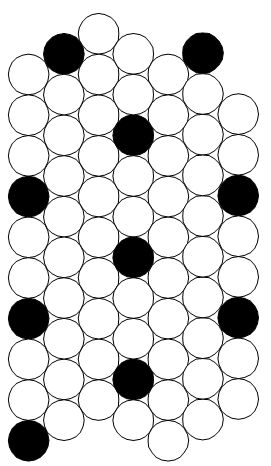
Figure 4. Perfect distribution of CSA atoms (dark) at substitutional sites in a hcp lattice.
To achieve the same volume concentration, another surface layer would have to be created 2 atomic thicknesses away. This seems achievable with the proper experimental setup.
The conclusion is that the sublimation concentration technique should allow practical preparation of the atomic concentrations appropriate for achieving a large increase in propellant Isp. Real target propellant concentrations are perhaps 7% Li in H23.
VIII. Experimental Verification
The experimental realization of the sublimation concentration process has been described for the most part in previous papers by the author10,11.
The primary, more recent, additional innovation is the use of using cold gaseous He to carry the CSA atoms to the condensing surface so that these atoms condense onto the solid with low thermal energy. One can calculate the approximate depositing gas temperature necessary to prevent penetration of the surface during deposition. For solid H2, first assume that the binding energy for the H2 dimer is 2.9 cm-1 = 4 K = 6 x 10-23 Joules. This is somewhat consistent with the 89 K sublimation energy - breaking the equivalent of about 20 dimers. The energy of a gas atom is 3kT/2, where k is the Boltzmann constant (1.4 x 10-23 J/K), and T is the temperature in Kelvins. Thus an atom at a temperature of about 3 K would have enough energy to break a H2-H2 dimer. Clearly if the temperature of the energetic atom can be brought to the temperature of gas above liquid helium, penetration into the matrix would not be significant.
Another feature of the experiment will be to anneal the grown crystals to remove defects. Quantitative research on the recrystallization rate of H2 is lacking. Experiments at the Institute for Low Temperature (ILT, Kharkov, Ukraine) have shown that the recrystallization rate of H2 must be relatively large, because fine-grained H2 samples could not be created13. A sample of solid H2 grown with 1 cm dimensions over one hour gave grain dimensions within the crystal of about 1 mm. Under slower growth rates (hours) 1 cm3 samples became single crystals.
The laboratory feasibility experiment will be performed at pressures of less than 10-5 torr so that there is no possibility of vapor (H2s or reacted dimers) impinging on the surface to impede the sublimation process. The surface temperature will rapidly equilibrate to the pressure, since sublimation will cool the surface such that it reaches the temperature associated with the vapor pressure established by the pumping speed. Heat transfer through solid H2 is very poor, so there will be a small, but significant thermal gradient in the solid that supplies the heat of sublimation to the surface.
An interesting conclusion of the present study is that the concentration limits will depend on the reaction distance, which, in turn, depends on the atomic species themselves. For instance the reaction distance for carbon (C) atoms will be significantly longer than that for lithium atoms, and boron may be stable at smaller distances. This suggests that the initial target atom experimentally should combine minimal reaction distance with ease of use; the most attractive candidate at this time is lithium, although boron is more attractive theoretically.
The primary process diagnostic will be spectroscopic measurement of the number of CSA atoms, and laser interferometric measurement of the position of the solid H2 surface. Interferometery using a HeNe laser will provide 100 nm resolution, which will be enough to see the surface retreat from sublimation. As the CSA atoms react and the dimers sublime from the surface, simple area absorption measurements of the remaining atom concentration will establish both the initial and final atom number of CSA atoms, which will establish the final surface concentration. When the concentration process is complete, the atom number will remain constant.
Once the concentrated layer has been formed as evidenced by a stable sublimation rate, the solid H2 can be heated slightly, the atoms allowed to react, and the heat/pressure release can then be used to confirm the stable atom concentration achieved.
IX. Engineering Implications
The justification and goal of the continuing present work on CSA sublimation concentration is to make major improvements in chemical propulsion. In the best case the increase in Isp gained by using a CSA may permit radical transformations in the economics and design of earth-to-orbit vehicles. The short term goal is that the cost to add and concentrate a CSA in a propellant will be more than paid for by a reduction in payload cost per unit mass resulting from the use of an enhanced propellant. The economics have been discussed in a previous paper11.
Sublimation concentration is fundamentally a surface process, whereas a high volume concentration is needed to form a superior propellant. One route to such a high volume concentration of CSA is to create sequential multiple concentrated CSA layers using repeated applications of the sublimation concentration technique. Each new deposition layer can be isolated from the previous concentrated layer by adding an insulating layer of H2s that is sublimed away from beneath the concentrating CSA atoms. Sublimation concentration of each new layer proceeds as before. Theoretical target concentrations are for example 7% Li in H23; even this high volume concentration may be achievable technically using this technique.
X. Conclusions
Modeling and investigation of the cryostabilized additive sublimation concentration process indicates that it should be able to provide a process for achieving relatively high concentration atom mixtures in solid hydrogen. Sublimation eliminates the mobile layer normally present on the surfaces of solid hydrogen above 3 K and allows removal of enough hydrogen matrix molecules to concentrate reactive atoms that have been previously deposited stably at low concentration. The concentration process is fundamentally stable, since any atoms that do react are at the surface and are sublimed away, leaving a stable surface behind. By continuing the sublimation and removing the close, reacting atoms, the randomness of the surface distribution is gradually removed, leaving and evenly distributed surface layer of high concentration atoms. Multiple deposition and sublimation processes can be used to create high atom volume concentrations for use engineering use as propellant.
Examining a model of the physics of the sublimation concentration has led to important insights into the process. The primary conclusions are that the process is a fundamentally stable technique for achieving high concentrations of cryostabilized atoms in solid hydrogen. Stability arises from stable reaction and sublimation of pairs of atoms that approach each other at the surface. Removal of excited dimers, by eliminating close pairs, allows the creation of a uniformly dispersed layer of atoms to be created, avoiding the limitations on concentration that normally arise due to reactions caused by the necessary statistical fluctuations of a deposition process.
Assuming lithium as a energetic atom at substitutional sites in solid hydrogen, modeling indicates that the reaction distance between atoms is 2 atomic diameters. Based on this reaction distance, surface atomic concentrations on the order of 10 atom % appear to be experimentally achievable, and above 5 atom % volume concentration with multiple sublimation concentration procedures. If accurate, this would provide desired target atom concentrations for a revolutionary improvement in chemical propellant Isp.
Acknowledgments
This work has been done under the sole support of Thoughtventions Unlimited LLC.
References
1. A.J. Barnes, W.J. Orville-Thomas, A. Muller, and R. Gaufres Eds., Matrix Isolation Spectroscopy, Reidel, Dordrecht, Germany, 1981.
2. Fajardo, M. E., "Matrix isolation of metal atoms generated by laser ablation. II. The Li/Ne, Li/D2 and Li/H2 systems," J. Chem. Phys., Vol. 98, No. 1, 1993, p. 110.
3. Carrick, P. G., "Theoretical Performance of Atomic and Molecular HEDM Additives to Solid H2," Proc. of the HEDM Conf., T.L. Thompson, Ed., 6-8 June 1993, Woods Hole, MA, USAF Phillips Lab Report,PL-TRS93-3041, 1993.
4. Jang, S., and Voth, G.A., "Lithium impurity recombination in solid para-hydrogen: A path integral quantum transition state theory study," J. Chem. Phys., Vol. 108, No. 10, 1998, p. 4098.
5. Scharf, D., Martyna, G.J., Voth, G.A., and Klein, M.L., "Nature of lithium trapping sites in the quantum solids para-hydrogen and ortho-deuterium," J. Chem. Phys., Vol. 99, No. 11, 1993, p. 9013.
6. Ishmoto, S., Kobayashi, T., Morimoto, K., Nomura, I., Ozawa, A., Suzuki, S., Takahashi, Y., Tanihata, I., and Tsuru, T., "Windowless solid hydrogen target," Nuclear Instr. Methods in Phys. Rsch A, Vol. 480, 2002, p. 304.
7. Albrech, U., Conradt, R., Herminghaus, S., and Leiderer, P., "Wetting Phenomena in films of molecular hydrogen isotopes," Low Temp. Phys., Vol. 22, No. 2, 1996, p. 117.
8. Bloss, E., and Wyatt, A.F.G., "Surface Diffusion of Solid Hydrogen," J. Low Temp. Phys., Vol. 119, No. 5/6, 2000, p. 743.
9. Jang, S., Jang, S., and Voth, G. A., "Quantum Molecular Dynamics Simulations of Low Temperature High Energy Density Matter: Solid p-H2/Li and p-H2/B," J. Phys. Chem. A, Vol. 103, 1999, p. 9512.
10. Bates, S.C., "Cryostabilized Propellant Additives," AIAA Paper AIAA-2003-5213, 2003.
11. Bates, S.C., "Techniques in Cryostabilized Additive Concentration," AIAA Paper AIAA-2004-4038, 2004.
12. Danilychev, A.V., and Apkarian, V.A., "Atomic oxygen in deuterium," Low Temperature Phys., Vol. 26, No. 9-10, 2000, pp. 669-678.
13. Manzhelii, V. G., and Freiman, Y. A., Eds., Physics of Cryocrystals, Amer. Inst. of Physics, Woodbury, NY, 1996.
14. Roder, H. M., Childs, G. E., McCarty, R.D., and Angerhofer, P.E., "Survey of the Properties of the Hydrogen Isotypes Below Their Critical Temperature," NBS Technical Note 641, 1973.